Question

An English professor assigns letter grades on a test according to the following scheme. A: Top 13% of scores B: Scores below the top 13% and above the bottom 60% C: Scores below the top 40% and above the bottom 24% D: Scores below the top 76% and above the bottom 8% F: Bottom 8% of scores Scores on the test are normally distributed with a mean of 77.4 and a standard deviation of 7.9. Find the numerical limits for a D grade. Round your answers to the nearest whole number, if necessary.

Answer 1

The numerical limits for a D grade are about 66 and 72 (rounding to the nearest whole number).

Explanation:

To answer the question, we need to find those values for x so that scores are below the top 76% and above the bottom 8%.

Well, those scores below the top 76% are the same that those scores below 24%. In other words, we need to find the percentile x, the value which divides in such a way the distribution that 76% of the values are above it and 24% of them are below it, or the 24th percentile.

Likewise, we also need to find the percentile 8th to find the lower limit for a D grade (or a value of x below it are the 8% of the cases).

For this, we need to consult the standard normal table to find which z-score corresponds to those probabilities corresponding to the limits values we are looking for.

We have to remember that a z-score 'transform' a raw score in values equivalent to a distance from the population mean, and in this way, we can consult the probabilities for any normally distributed data. The formula for a z score is:

`\\ z = (x - \mu)/(\sigma)` (1)

Where

`\\ x\;is\;the\;raw\;score`.

`\\ \mu\;is\;the\;population\;mean`.

`\\ \sigma\;is\;the\;population\;standard\;deviation`.

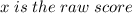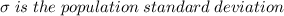Finding the Upper limit for D grade

To find the 24th percentile using the cumulative standard normal table, we already know that the normal distribution is symmetrical as well as the standard normal distribution.

The question is, what is the value of z for which 24 percent of the cases are below it? If we consult the cumulative standard normal table for the probability of 0.76 (1 - 0.24 = 0.76), we obtain an approximate value for z = 0.7.

Then, we know that P(z<0.7) = 0.76 or P(z>0.7) =0.24. Because of the symmetry of the normal distribution P(z<-0.7) = 0.24. The negative symbol for z is because this score is below the mean of the distribution.

Using (1), we can solve the equation for x, to determine the 24th percentile or the upper limit for D grade.

`\\ -0.7 = (x - 77.4)/(7.9)`

`\\ -0.7 * 7.9 =x - 77.4`

`\\ (-0.7 * 7.9) + 77.4 = x`

`\\ 71.87 = x`

`\\ x = 71.87\;or\;\approx 72`

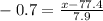
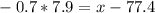
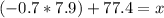
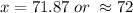
Then, the upper limit for D grade is 72 (rounding to the nearest whole number).

Finding the lower limit for D grade

To find the lower limit, we can follow the same steps.

Consulting the cumulative standard normal table, the value for z for a probability (1 - 0.08 = 0.92), we obtain a value of z = 1.40. Because of the symmetry of the normal distribution, a score of z = -1.40 give the values P(z<-1.40) = 0.08.

Again, using (1), we can solve the equation for x, to determine the 8th percentile or the lower limit for D grade.

`\\ -1.40 = (x - 77.4)/(7.9)`

`\\ -1.40 * 7.9 = x - 77.4`

`\\ (-1.40 * 7.9) + 77.4 = x`

`\\ 66.34 = x`

`\\ x = 66.34 \approx 66`

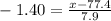
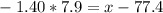
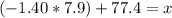
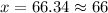
Then, the lower limit for D grade is 66 (rounding to the nearest whole number).

In the graph below, the blue shaded area is between the raw scores 66 and 72, approximately.