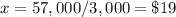Question

A baseball team plays in a stadium that holds 55,000 spectators. With the ticket price at $10, the average attendance at recent games has been 27,000 . A market survey indicates that for every dollar the ticket price is lowered , attendance increases by 3000. (a) Find a function that models the revenue in terms of ticket price. (b) Find the price that maximizes revenue from ticket sales. (c) What ticket price is so high that no revenue is generated?

Answer 1

(a)
`R=-3,000x^2+57,000x`

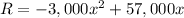
(b) x = $9.50

(c) x= $19

Step-by-step explanation:

Function Modeling

We frequently use mathematical functions to model the behavior of our quantitative realities. Scientists collect field data and use different methods to find the best function to model the changes in all the variables of the problem under study.

(a) The question states the relationship of the attendance in a stadium with the ticked price. We are using the following model for the attendance A in terms of the price x:

`A=mx+b`

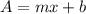
The values of m and b are to be found by using the conditions given in the question. For a price x=10, the attendance is A=27,000. This gives us a first point (10;27,000). We also know that for every dollar the ticked price is lowered, attendance increases by 3,000. This gives us a second point (9;30,000). Let's plug them in into the equation

`27,000=m\cdot 10+b`

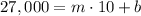
This gives us the equation

`10m+b=27,000`

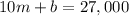
Now for the second point

`30,000=m\cdot 9+b`

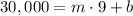
That produces the equation

`9m+b=30,000`

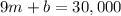
Subtracting both equations, we have

`m=-3,000`

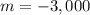
Solving for b in the first equation

`b=27,000-10m=27,000+10\cdot 3,000=57,000`

`b=57,000`

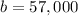
Thus, the equation is

`A=-3,000x+57,000`

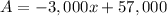
The revenue function is the number of tickets sold times the price of each ticket, thus

`R=A.x=-3,000x^2+57,000x`

`R=-3,000x^2+57,000x`

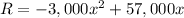
(b) To find the price that maximized the revenue, we use derivatives. Computing R':

`R'=-6,000x+57,000`

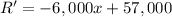
We now equate R'=0

`-6,000x+57,000=0`

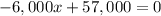
Which gives us the value

`x=57,000/6=\$ 9.5`

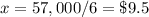
We'll find out it this produces a maximum or a minimum, computing R''

`R''=-6,000`

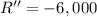
Since R'' is negative, the price of $9.50 produces a maximum in the revenue function.

(c) We must find the ticket price that produces no revenue, that is

`-3,000x^2+57,000x=0`

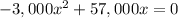
Simplifying by x

`-3,000x+57,000=0`

Solving for x

`x=57,000/3,000=\$ 19`