Question

Thirty percent of the CFA candidates have a degree in economics. A random sample of three CFA candidates is selected. What is the probability that none of them has a degree in economics?

Answer 1

0.343

Step-by-step explanation:

Given that,

Percent of CFA candidates have a degree in economics, p = 30% = 0.3

Random sample of CFA candidates, n = 3

Here, we are using the binomial distribution.

Let X be the number of CFA candidates having economics degree.

Probability that none of them has a degree in economics, P(X = 0) :

=
`\binom{n}{0}p^(0)(1-p)^(n-0)`

=
`\binom{3}{0}(0.3)^(0)(1-0.3)^(3-0)`

=
`1* 1 * (0.7)^(3)`

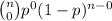
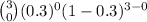
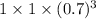
= 0.343

Therefore, the probability that none of them has a degree in economics is 0.343.