Question

According to the article "Characterizing the Severity and Risk of Drought in the Poudre River, Colorado" (J. of Water Res. Planning and Mgmnt., 2005: 383–393), the drought length Y is the number of consecutive time intervals in which the water sup- ply remains below a critical value yo (a deficit), pre- ceded by and followed by periods in which the supply exceeds this critical value (a surplus). The cited paper proposes a geometric distribution with p = .409 for this random variable.

a. What is the probability that a drought lasts exactly 3 intervals? At most 3 intervals?

b. What is the probability that the length of a drought exceeds its mean value by at least one standard deviation?

Answer 1

(a) P (Y = 3) = 0.0844, P (Y ≤ 3) = 0.8780

(b) The probability that the length of a drought exceeds its mean value by at least one standard deviation is 0.2064.

Explanation:

The random variable Y is defined as the number of consecutive time intervals in which the water supply remains below a critical value y₀.

The random variable Y follows a Geometric distribution with parameter p = 0.409.

The probability mass function of a Geometric distribution is:

`P(Y=y)=(1-p)^(y)p;\ y=0,12...`

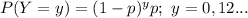
(a)

Compute the probability that a drought lasts exactly 3 intervals as follows:

`P(Y=3)=(1-0.409)^(3)* 0.409=0.0844279\approx0.0844`

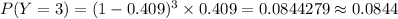
Thus, the probability that a drought lasts exactly 3 intervals is 0.0844.

Compute the probability that a drought lasts at most 3 intervals as follows:

P (Y ≤ 3) = P (Y = 0) + P (Y = 1) + P (Y = 2) + P (Y = 3)

`=(1-0.409)^(0)* 0.409+(1-0.409)^(1)* 0.409+(1-0.409)^(2)* 0.409\\+(1-0.409)^(3)* 0.409\\=0.409+0.2417+0.1429+0.0844\\=0.8780`

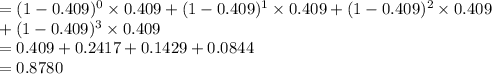
Thus, the probability that a drought lasts at most 3 intervals is 0.8780.

(b)

Compute the mean of the random variable Y as follows:

`\mu=(1-p)/(p)=(1-0.409)/(0.409)=1.445`

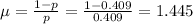
Compute the standard deviation of the random variable Y as follows:

`\sigma=\sqrt{(1-p)/(p^(2))}=\sqrt{(1-0.409)/((0.409)^(2))}=1.88`

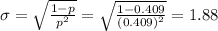
The probability that the length of a drought exceeds its mean value by at least one standard deviation is:

P (Y ≥ μ + σ) = P (Y ≥ 1.445 + 1.88)

= P (Y ≥ 3.325)

= P (Y ≥ 3)

= 1 - P (Y < 3)

= 1 - P (X = 0) - P (X = 1) - P (X = 2)

`=1-[(1-0.409)^(0)* 0.409+(1-0.409)^(1)* 0.409\\+(1-0.409)^(2)* 0.409]\\=1-[0.409+0.2417+0.1429]\\=0.2064`

Thus, the probability that the length of a drought exceeds its mean value by at least one standard deviation is 0.2064.