Question

a) Calculate the modulus of elasticity of carbon-epoxy composite under isostrain condition if the composite consists of 40% carbon fibers and 60% epoxy by volume. Also, b) calculate the percentage of load carried by the carbon fibers. The modulus of elasticity of the carbon fibers and the epoxy are 350 GPa and 3.5 GPa, respectively. If a longitudinal stress of 60 MPa is applied on the composite with a cross-sectional area of 250 mm2 , c) what is the load carried by each of the fiber and the matrix phase

Answer 1

Part (a)

Eₓ = 142.1 GPa

Part (b)

Load carried by carbon fiber = 98.5%

Part (c)

F (fiber) = 14776.1 N

F (matrix) = 221.63 N

Step-by-step explanation:

Given data:

Carbon-Epoxy composite

Carbon fibers = 40%

Epoxy fibers = 60%

Modulus of elasticity of carbon fibers = 350 GPa

Modulus of elasticity of Epoxy fibers = 3.5 GPa

Longitudinal stress = 60 MPa

Cross-sectional area = 250 mm^2

Solution:

Part (a)

Modulus of Elasticity of composite material = Eₓ = E₁V₁ + E₂V₂

Eₓ = Modulus of Elasticity of composite material

E₁ = Modulus of Elasticity of carbon fibers

V₁ = % of carbon fibers

E₂ = Modulus of Elasticity of epoxy fibers

V₂ = % of epoxy fibers

Eₓ = 350*0.4 + 3.5*0.6

Eₓ = 142.1 GPa

Part (b)

Load carried by carbon fiber

`F carbon / F composite = (Ecarbon*Vcarbon) / (E composite * V composite)`

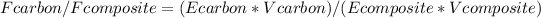
Put,

V composite = 1

E composite = 142.1 GPa

E carbon = 350 GPa

V carbon = 0.4

= (350*0.4) / (142.1*1)

= 0.985

Load carried by carbon fiber = 98.5%

Part (c)

First calculate ratio of fiber load to matrix load

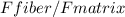`F fiber /F matrix` = (350*0.4) / (3.5*0.6) (F represents force or load)

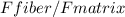`F fiber /F matrix` = 66.67 ................... Eq (1)

`F fiber = 66.67 * F matrix`

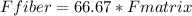
Total force sustained by composite material

= Applied stress * Cross-sectional area

Fₓ = 60 MPa * 250 mm^2

Fₓ = 15,000 N

This total load is carried by both fibers and matrix phases. So,

Fₓ = F (fiber) + F (matrix)

Put values in above equation

15,000 = (66.67 * F (matrix)) + F (matrix)

15,000 = 67.67 F (matrix)

F (matrix) = 221.63 N

Put F (matrix) = 221.63 N in equation (1)

F (fiber) = 221.63 * 66.67

F (fiber) = 14776.1 N