Answer:
The expression for the perimeter P is
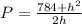 feet.
feet.
Area=49=lx square feet ( here
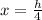 )
)
Explanation:
Given that rectangle with height equals 4times width.
It can be written as

Let x be the width of the given rectangle
Therefore
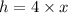
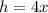
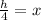
Rewritting the above equation we get
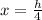
To write an expression for the perimeter P of the given rectangle :
Also given that area of the rectangle is 49 square feet.
Area=49 square feet.
We know area of rectangle = lw square units.
Therefore area=49=lx square feet ( here area=49 and w=
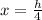 )
)
Rewritting we get
lx=49 square feet.
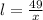
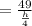
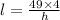
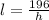 feet
feet
Perimeter P
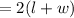 units
units

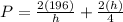
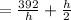

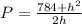 feet.
feet.