Answer:
a)
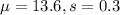
b)
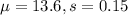
c) Option A) The mean of the sampling distribution stays the same, but the standard deviation decreases
Explanation:
We are given the following in the question:
Population mean,
 = 13.6
= 13.6
Standard deviation,
 = 3.0
= 3.0
a) Sample size, n = 100
The mean of the sampling distribution is best approximated by population mean.
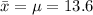
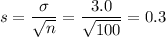
b) Sample size, n = 400
The mean of the sampling distribution is best approximated by population mean.
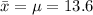

c) Thus, we observed as the sample size increases the standard deviation increases.
Thus, the correct answer is:
Option A) The mean of the sampling distribution stays the same, but the standard deviation decreases