Question

A professor would like to test the hypothesis that the average number of minutes that a student needs to complete a statistics exam has a standard deviation that is less than 5.0 minutes. A random sample of 15 students was selected and the sample standard deviation for the time needed to complete the exam was found to be 4.0 minutes. What would be the number of degrees of freedom for this hypothesis​ test?

Answer 1

The number of degrees of freedom for this hypothesis​ test is 14.

Explanation:

In this case the professor wants to determine whether the average number of minutes that a student needs to complete a statistics exam has a standard deviation that is less than 5.0 minutes.

Then the variance will be,
`\sigma^(2)=(5.0)^(2)=25`

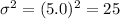
The hypothesis to determine whether the population variance is less than 25.0 minutes or not, is:

H₀: The population variance is not less than 25.0 minutes, i.e. σ² = 25.

Hₐ: The population variance is less than 25.0 minutes, i.e. σ² < 25.

The test statistics is:

`\chi ^(2)_(cal.)=(ns^(2))/(\sigma^(2))`

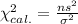
The decision rule is:

If the calculated value of the test statistic is less than the critical value,
`\chi^(2)_((1-\alpha), (n-1))` then the null hypothesis will be rejected.

Here,

α = level of significance

(n - 1) = degrees of freedom

The degrees of freedom is the number of values that can change throughout a statistical hypothesis test.

Compute the degrees of freedom as follows:

`df=n-1=15-1=14`

Thus, the number of degrees of freedom for this hypothesis​ test is 14.