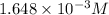Question

2 H2S(g) ⇄ 2 H2(g) + S2(g) Kc = 9.3× 10-8 at 400ºC 0.47 moles of H2S are placed in a 3.0 L container and the system is allowed to reach equilibrium. Calculate the concentration of H2 at equilibrium.

Answer 1

Answer: The concentration of hydrogen gas at equilibrium is
`1.648* 10^(-3)M`

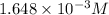
Step-by-step explanation:

We are given:

Initial moles of hydrogen sulfide gas = 0.47 moles

Volume of the container = 3.0 L

The molarity of solution is calculated by using the equation:

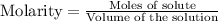
`\text{Molarity}=\frac{\text{Moles of solute}}{\text{Volume of the solution}}`

So,
`\text{Initial molarity of hydrogen sulfide gas}=(0.47)/(3)=0.1567M`

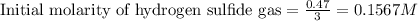
The given chemical equation follows:

`2H_2S(g)\rightleftharpoons 2H_2(g)+S_2(g)`

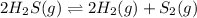
Initial: 0.1567

At eqllm: 0.1567-2x 2x x

The expression of
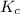`K_c` for above equation follows:

`K_c=([H_2]^2[S_2])/([H_2S]^2)`

We are given:

`K_c=9.3* 10^(-8)`

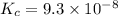
Putting values in above equation, we get:

`9.3* 10^(-8)=((2x)^2* x)/((0.1567-2x)^2)\\\\x=8.24* 10^(-4)`

So, equilibrium concentration of hydrogen gas =
`2x=(2* 8.24* 10^(-4))=1.648* 10^(-3)M`

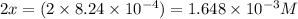
Hence, the concentration of hydrogen gas at equilibrium is
`1.648* 10^(-3)M`