Question

A rotating wheel requires 3.05-s to rotate through 37.0 revolutions. Its angular speed at the end of the 3.05-s interval is 97.9 rad/s. What is the constant angular acceleration of the wheel?

Answer 1

`\alpha=14.2rad/s^2`

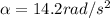
Step-by-step explanation:

The formula that relates angular displacement with angular acceleration is:

`\Delta \theta=\omega_i t+(\alpha t^2)/(2)`

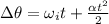
We can obtain
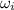`\omega_i` from the definition of angular acceleration:

`\alpha=(\Delta \omega)/(\Delta t)=(\omega_f-\omega_i)/(t)`

`\omega_i=\omega_f-\alpha t`

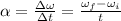
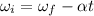
Putting all together:

`\Delta \theta=(\omega_f-\alpha t) t+(\alpha t^2)/(2)=\omega_f t-(\alpha t^2)/(2)`

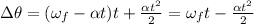
Which, since we want the angular acceleration, is:

`\alpha=(2(\omega_f t-\Delta \theta))/(t^2)`

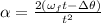
And for our values is:

`\alpha=(2((97.9rad/s)(3.05s)-(37(2\pi rad))))/((3.05s)^2)=14.2rad/s^2`