Question

At the top of a giant swing on the high bar, a 50 kg gymnast’s velocity is 3 m/s, and he is 3.5 m high. What is the gymnast’s total mechanical energy (KE + PE+ SE) at this instant?

Answer 1

Total Mechanical Energy of the gymnast = 1940J = 1.94 kJ

Step-by-step explanation:

Total Mechanical Energy = KE + PE + SE

Kinetic Energy,
`KE = 1/2 MV^(2)`

`KE = 0.5 * 50 * 3^(2) \\KE = 225 J`

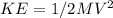
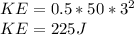
Potential Energy,

`PE = mgh\\PE = 50 * 9.8 * 3.5\\\\PE=1715 J`

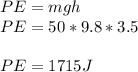
Strain Energy,

`SE = 1/2 K x^(2)`

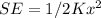
Since there is no force of deformation, x = 0, SE = 0

Total Mechanical Energy = 225 + 1715

Total Mechanical Energy of the gymnast = 1940J = 1.94 kJ