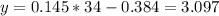Answer:
a)
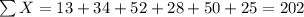
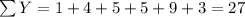

And in order to calculate the correlation coefficient we can use this formula:
![r=(n(\sum xy)-(\sum x)(\sum y))/(√([n\sum x^2 -(\sum x)^2][n\sum y^2 -(\sum y)^2]))](https://img.qammunity.org/2021/formulas/mathematics/college/etwpz2m1hveafk1jrc9rinpvxjo6l2hlwm.png)
![r=(6(1074)-(202)(27))/(√([6(7938) -(202)^2][6(157) -(202)^2]))=0.821](https://img.qammunity.org/2021/formulas/mathematics/college/mzexicv7mcka3btjc6b3cdq9gyfnqq1f2h.png)
b)
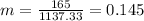
Nowe we can find the means for x and y like this:
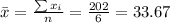
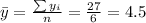
And we can find the intercept using this:

So the line would be given by:
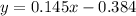
c) The coefficient of variation is given by:
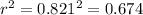
And we can conclude that 67.4% of the variation in y can be explainedby the corresponding variation in x and the least-squares line
d) For this case we just need to replade x = 34 into our model and we got:
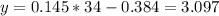
Explanation:
For this case we have the following data:
x 13 34 52 28 50 25
y 1 4 5 5 9 3
Part a
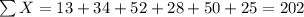
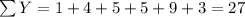

And in order to calculate the correlation coefficient we can use this formula:
![r=(n(\sum xy)-(\sum x)(\sum y))/(√([n\sum x^2 -(\sum x)^2][n\sum y^2 -(\sum y)^2]))](https://img.qammunity.org/2021/formulas/mathematics/college/etwpz2m1hveafk1jrc9rinpvxjo6l2hlwm.png)
![r=(6(1074)-(202)(27))/(√([6(7938) -(202)^2][6(157) -(202)^2]))=0.821](https://img.qammunity.org/2021/formulas/mathematics/college/mzexicv7mcka3btjc6b3cdq9gyfnqq1f2h.png)
Part b
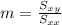
Where:

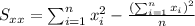
With these we can find the sums:
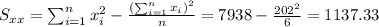
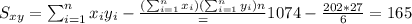
And the slope would be:
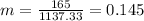
Nowe we can find the means for x and y like this:
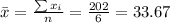
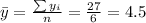
And we can find the intercept using this:

So the line would be given by:
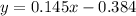
Part c
The coefficient of variation is given by:
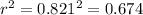
And we can conclude that 67.4% of the variation in y can be explainedby the corresponding variation in x and the least-squares line
Part d
For this case we just need to replade x = 34 into our model and we got: