Question

A sporting goods store believes the average age of its customers is 38 or less. A random sample of 40 customers was​ surveyed, and the average customer age was found to be 41.6 years. Assume the standard deviation for customer age is 8.0 years. Using alphaequals0.05​, complete parts a and b below. a. Does the sample provide enough evidence to refute the age claim made by the sporting goods​ store? Determine the null and alternative hypotheses. Upper H 0​: mu less than or equals 38 Upper H 1​: mu greater than 38 The​ z-test statistic is 2.85. ​(Round to two decimal places as​ needed.) The critical​ z-score(s) is(are) 1.64. ​(Round to two decimal places as needed. Use a comma to separate answers as​ needed.) Because the test statistic is greater than the critical value, reject the null hypothesis. b. Determine the​ p-value for this test. The​ p-value is . 998. ​(Round to three decimal places as​ needed.)

Answer 1

Test statistics = 2.85

P-value = 0.002

Explanation:

We are given that a sporting goods store believes the average age of its customers is 38 or less.

A random sample of 40 customers was​ surveyed, and the average customer age was found to be 41.6 years and the standard deviation for customer age is 8.0 years.

Null Hypothesis,
`H_0` :
`\mu` <= 38 years

Alternate Hypothesis,
`H_1` :
`\mu` > 38 years

The test statistics we will use here is;

T.S. =
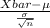`(Xbar-\mu)/((\sigma)/(√(n) ) )` ~ N(0,1)

where, X bar = sample mean = 41.6 years

`\sigma` = population standard deviation = 8 years

n = sample size = 40

So, test statistics =
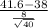`(41.6-38)/((8)/(√(40) ) )` = 2.85

At 5% level of significance, the z table gives critical value of 1.6449. Since our test statistics is more than the critical value of z so we have sufficient evidence to reject the null hypothesis and conclude that average age of its customers is more than 38 years.

P-value is given by, P(Z > 2.85) = 1 - P(Z <= 2.85) = 1 - 0.99781 = 0.002 .