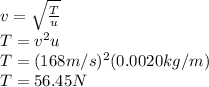Answer:
(a)
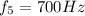
(b)
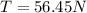
Step-by-step explanation:
For part (a)
The wave with three antinodes has m=3.Thus f₃=3f₁ and so the fundamental frequency of string is:
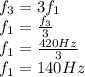
Thus the frequency of fifth harmonic is
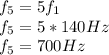
For Part (b)
The speed of transverse wave on this string is related to the fundamental frequency by:
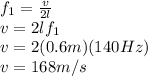
As the speed of wave is related to tension of string and its linear density by: