Answer:
Explanation:
Consider the equation of the curve,
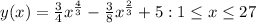
Find the arc length directly as follows:
Arc length of the curve:
if
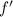 is continous on [a,b], then the length of the curve
is continous on [a,b], then the length of the curve
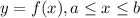 is
is
![L=\int\limits^b_a {\sqrt{1+[(dy)/(dx) ]^2} } \, dx](https://img.qammunity.org/2021/formulas/mathematics/college/5mbmolsckfmxmd29sy79ua52isznqbxws5.png)
Differentiate the function with respect to x,
![(dy)/(dx)= (d)/(dx)[(3)/(4)^{(4)/(3) }-(3)/(8)^{(2)/(3) }+5]\\\\=(d)/(dx)[(3)/(4)^{(4)/(3) }]-(d)/(dx)[(3)/(8)^{(2)/(3) }]+(d)/(dx)(5)\\\\=(3)/(4) (d)/(dx)[x^{(4)/(3)}] -(3)/(8) (d)/(dx)[x^{(2)/(3)}]+(d)/(dx)(5)\\ \\=(3)/(4)[(4)/(3)x^{(1)/(3) } ] +(3)/(8)[(2)/(3)x^{(1)/(3) } ]+0\\ \\=x^{(1)/(3)}-(1)/(4)x^{(1)/(3)}](https://img.qammunity.org/2021/formulas/mathematics/college/dv2akuea35d5n3r4ogg1h32jlv7ww3sc1u.png) use
use
![(d)/(dx)[x^n]=nx^(n-1)](https://img.qammunity.org/2021/formulas/mathematics/college/it06eqek6aqxo29g21zupn1npa7v6tqlet.png)
That is,
![((dy)/(dx) )^2=(x^{(1)/(3) }-(1)/(4)x^(1)/(3) )^2\\\\=x^{(1)/(3) }+(1)/(16)x^{(1)/(3) }-(1)/(2)\\\\\sqrt{1+[(dy)/(dx) ]^2}=\sqrt{1+x^{(1)/(3) }+(1)/(16)x^{(1)/(3) }-(1)/(2)} \\\\ =\sqrt{x^{(1)/(3) }+(1)/(16)x^{(1)/(3) }+(1)/(2)}](https://img.qammunity.org/2021/formulas/mathematics/college/4wpkfny01q1r0wp98et4qqwvgecbfu51h7.png)
since
![[x^{(1)/(3)}+(1)/(4)x^{-(1)/(3)}]^2=x^{(1)/(3)}+(1)/(16)x^{-(2)/(3)}+(1)/(2)](https://img.qammunity.org/2021/formulas/mathematics/college/bbtzixsaqdk3tlq0lj3z3i4pdyaxc3rc0b.png)
![=[x^{(1)/(3)}+(1)/(4)x^{-(1)/(3)}]^2\\\\=x^{(1)/(3)}+(1)/(4)x^{-(1)/(3)}](https://img.qammunity.org/2021/formulas/mathematics/college/z98owbac0vt4a9ae4h8mznk1tvzrg9fna0.png)
substitute this value in arc length formula to get,
![L=\int\limits^(27)_1 {[x^{(1)/(3)}]+(1)/(4)x^{-(1)/(3)}} \, dx \\\\=\int\limits^(27)_1 {[x^{(1)/(3)}]\, dx + (1)/(4)\int\limits^(27)_1 [x^{-(1)/(3)}}] \, dx\\\\=(3)/(4) [x^{(1)/(3)}]\limits^(27)_1 + (1)/(4) [(3)/(2)x^{(1)/(3)}]\limits^(27)_1](https://img.qammunity.org/2021/formulas/mathematics/college/5fufifrwionm3xtc26l3t5wb4s43q6t36m.png)
use
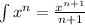
![=(3)/(4) [27^{(4)/(3) }-1]+(3)/(8) [27^{(2)/(3)}-1]\\\\=63](https://img.qammunity.org/2021/formulas/mathematics/college/qzm3o79laoak6mwu25peyyya5x6l3jjhq8.png)
therefore the length of the curves is L=63