Question

26. A single-turn wire loop is 2.0 cm in diameter and carries a 650- mA current. Find the magnetic field strength (a) at the loop center and (b) on the loop axis, 20 cm from the center. Wolfson, Richard. Essential University Physics, Volume 2 (p. 511). Pearson Education. Kindle Edition.

Answer 1

(a) Magnetic field at the center of the loop is 4.08 x 10⁻⁵ T

(b) Magnetic field at the axis of the loop is 5.09 x 10⁻⁹ T

Step-by-step explanation:

Given :

Diameter of the circular loop = 2 cm

Radius of the circular loop, R = 1 cm = 0.01 m

Current flowing through the circular wire, I = 650 mA = 650 x 10⁻³ A

(a) Magnetic field at the center of circular loop is determine by the relation:

`B=(\mu_(0)I )/(2R)`

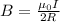
Here μ₀ is vacuum permeability constant and its value is 4π x 10⁻⁷ T m²/A.

Substitute the suitable values in the above equation.

`B=(4\pi*10^(-7)*650*10^(-3) )/(2*0.01)`

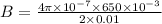
B = 4.08 x 10⁻⁵ T

(b) Distance from the center of the loop, z = 20 cm = 0.2 m

Magnetic field at the point on the axis of the loop is determine by the relation:

`B=(\mu_(0)IR^(2) )/(2(z^(2)+R^(2))^(3/2) )`

`B=(4\pi*10^(-7)*650*10^(-3)* (0.01)^(2) )/(2((0.2)^(2)+(0.01)^(2))^(3/2) )`

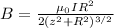
B = 5.09 x 10⁻⁹ T