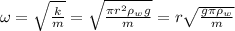Question

A cylindrical piece of wood of height H, radius r, and uniform density rhoc is bobbing up and down in still water with its axis aligned vertically. The density of the water is rhow. Gravity acts vertically downward on the wood with magnitude mg, where m is the wood’s mass. Neglecting friction, the motion of the bobbing wood about its equilibrium depth can be described by A cos (ωt + φ), a function of time t. What is ω?

Answer 1

`r\sqrt{(g\pi\rho_w)/(m)}`

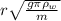
Step-by-step explanation:

As the buoyant force is proportional to the length of which the wood is submerged in water, we can model the buoyant force as a spring force and the bobbing wood is a simple harmonic motion described as A cos (ωt + φ) where

`\omega = \sqrt{(k)/(m)}`

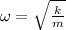
where k (N/m) is the "spring" buoyant constant and m is the mass of wood

The buoyant force is basically the weight of water displaced by the submerged wood, which is the gravity acting on the cylindrical volume

`F_b = W_w = m_wg = V_w\rho_w g`

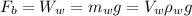
Since the cylindrical has a form of AL where A is the base area and L is the length submerged

`F_b = AL\rho_w g = (\pi r^2\rho_w g) L`

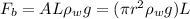
As L can be treated as the spring "stretched/compressed" length, the rest is k:

`F_b = kL = (\pi r^2\rho_w g) L`

`k = (\pi r^2\rho_w g)`

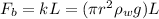
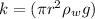
Therefore

`\omega = \sqrt{(k)/(m)} = \sqrt{(\pi r^2\rho_w g)/(m)} = r\sqrt{(g\pi\rho_w)/(m)}`