Question

Data from the article "The Osteological Paradox: Problems inferring Prehistoric Health from Skeletal Samples" (Current Anthropology (1992):343-370) suggests that a reasonable model for the distribution of heights of 5-year old children (in centimeters) is N(100, 62) . Let the letter X represent the variable "height of 5-year old", and use this information to answer the following. Use 4 decimal places unless otherwise indicated.

(a) P(X > 89.2) =
(b) P(X < 109.78) =
(c) P(97 < X < 106) =
(d) P(X < 85.6 or X > 111.4) =
(e) P(X > 103) =
(f) P(X < 98.2) =
(g) P(100 < X < 124)=
(h) The middle 80% of all heights of 5 year old children fall between and . (Use 2 decimal places.)

Answer 1

(a) P (X < 109.78) = 0.9484.

(b) P (X < 109.78) = 0.9484.

(c) P (97 < X < 106) = 0.5328.

(d) P (X < 85.6 or X > 111.4) = 0.0369.

(e) P (X > 103) = 0.3085.

(f) P (X < 98.2) = 0.3821.

(g) P (100 < X < 124) = 0.5000.

(h) The middle 80% of all heights of 5 year old children fall between 92.31 and 107.70.

Explanation:

It is provided that X follows a Normal distribution with mean, μ = 100 and standard deviation, σ = 6.

(a)

Compute the value of P (X > 89.2) as follows:

`P (X>89.2)=P((X-\mu)/(\sigma)>(89.2-100)/(6))\\=P(Z>-1.80)\\=P(Z<1.8)\\=0.9641`

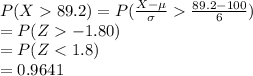
Thus, the value of P (X > 89.2) is 0.9641.

(b)

Compute the value of P (X < 109.78) as follows:

`P (X<109.78)=P((X-\mu)/(\sigma)<(109.78-100)/(6))\\=P(Z<1.63)\\=0.9484`

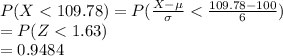
Thus, the value of P (X < 109.78) is 0.9484.

(c)

Compute the value of P (97 < X < 106) as follows;

P (97 < X < 106) = P (X < 106) - P (X < 97)

`=P((X-\mu)/(\sigma)<(106-100)/(6))+P((X-\mu)/(\sigma)<(97-100)/(6))\\=P(Z<1)-P(Z<-0.5)\\=0.8413-0.3085\\=0.5328`

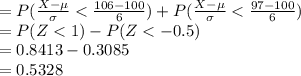
Thus, the value of P (97 < X < 106) is 0.5328.

(d)

Compute the value of P (X < 85.6 or X > 111.4) as follows;

P (X < 85.6 or X > 111.4) = P (X < 85.6) + P (X > 111.4)

`=P((X-\mu)/(\sigma)<(85.6-100)/(6))+P((X-\mu)/(\sigma)>(111.4-100)/(6))\\=P(Z<-2.4)-P(Z>1.9)\\=0.0082+0.0287\\=0.0369`

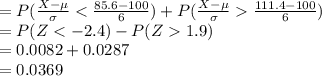
Thus, the value of P (X < 85.6 or X > 111.4) is 0.0369.

(e)

Compute the value of P (X > 103) as follows:

`P (X>103)=P((X-\mu)/(\sigma)>(103-100)/(6))\\=P(Z>0.50)\\=14-P(Z<0.50)\\=1-0.6915\\=0.3085`

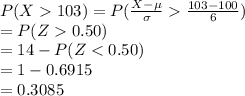
Thus, the value of P (X > 103) is 0.3085.

(f)

Compute the value of P (X < 98.2) as follows:

`P (X<98.2)=P((X-\mu)/(\sigma)<(98.2-100)/(6))\\=P(Z<-0.30)\\=1-P(Z<0.30)\\=1-0.6179\\=0.3821`

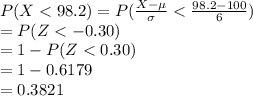
Thus, the value of P (X < 98.2) is 0.3821.

(g)

Compute the value of P (100 < X < 124) as follows;

P (100< X < 124) = P (X < 124) - P (X < 100)

`=P((X-\mu)/(\sigma)<(124-100)/(6))+P((X-\mu)/(\sigma)<(100-100)/(6))\\=P(Z<4)-P(Z<0)\\=1-0.50\\=0.50`

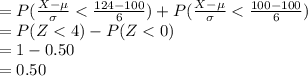
Thus, the value of P (100 < X < 124) is 0.5000.

(h)

Compute the value of x₁ and x₂ as follows if P (x₁ < X < x₂) = 0.80 as follows:

`P(X_(1)<X<x_(2))=P(X<x_(2))-P(X<x_(1))\\0.80=P(Z<z)-P(Z<-z)\\0.80=P(Z<z)-[1-P(Z<z)]\\0.80=2P(Z<z)-1\\1.80=2P(Z<z)\\P(Z<z)=0.90`

The value of z is ± 1.282.

The value of x₁ and x₂ are:

`-z=(x_(1)-\mu)/(\sigma) \\-1.282=(x_(1)-100)/(6)\\x_(1)=100-(6*1.282)\\=92.308\\\approx92.31`
`z=(x_(2)-\mu)/(\sigma) \\1.282=(x_(2)-100)/(6)\\x_(2)=100+(6*1.282)\\=107.692\\\approx107.70`

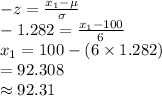
Thus, the middle 80% of all heights of 5 year old children fall between 92.31 and 107.70.