Complete question:
A pendulum of length L = 48.5 cm and mass m = 169 g is released from rest when the cord makes an angle of 65.4° with the vertical. What is the speed of the mass (m/s) upon reaching its lowest point?
Answer:
The speed of the mass upon reaching its lowest point is 2.36m/s
Step-by-step explanation:
To obtain the speed of the mass upon reaching its lowest point, we apply the principle of conservation of mechanical energy. At the lowest point, the kinetic energy of the pendulum is maximum and at the highest point, the vertical displacement is maximum, thus potential energy is maximum.
Kinetic energy at the lowest point = Potential energy at the highest point
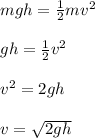
From my explanation above, h is the vertical displacement, when potential energy of the pendulum is maximum. Considering a right angled triangle, this vertical displacement, h is the adjacent of the triangle, and it is equal to
L - Lcosθ.
h = 48.5 - 48.5cos(65.4) = 28.31 cm = 0.2831 m

Therefore, the speed of the mass upon reaching its lowest point is 2.36m/s