Question

A bacteria culture initially contains 100 cells and grows at a rate proportional to its size. After an hour the population has increased to 570. (a) Find an expression for the number of bacteria after t hours. P(t) = (b) Find the number of bacteria after 4 hours. (Round your answer to the nearest whole number.) P(4) = bacteria (c) Find the rate of growth after 4 hours. (Round your answer to the nearest whole number.) P'(4) = bacteria per hour (d) When will the population reach 10,000? (Round your answer to one decimal place.)

Answer 1

See the explanation.

Explanation:

In one hour, the population has increased from 100 to 570.

The population becomes
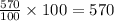`(570)/(100) * 100= 570`% of 100.

Hence, according to our observation, we can tell that the population of the bacteria grows up to 570% of previous hour.

(a)

The number of bacteria after t hours can be represented as
`p(t) = ((570)/(100) )^(t) * 100`.

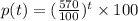(b)

After 4 hours, the number of bacteria will be
`((570)/(100) )^(4) * 100 = 105560.01`.

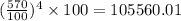(c)

The derivative of p(t) is
`100* ln(5.7) * (5.7)^t`.

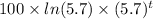At t = 4, the value will be 183723.6268 ≅ 183724.

(d)

The population will be 10,000 that is p(t) = 10000.

`(5.7)^t *100 = 10000\\(5.7)^t = 100\\t = 2.64594 = 2.6`.