Answer:
Test statistics = 2.578
Explanation:
We are given that the director of student health at a large university was concerned that students at his school were consuming too many calories each day. For a certain population of college-age students, it is recommended to consume around 2,000 calories/day.
Also, given Null Hypothesis,
 :
:
 = 2000
= 2000
Alternate Hypothesis,
 :
:
 > 2000
> 2000
The test statistics used here will be;
T.S. =
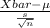 ~
~

where, X bar = sample mean = 2105 calories/day
s = sample standard deviation = 288 calories/day
n = sample of students = 50
So, test statistics =
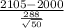 ~
~
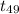
= 2.578
Therefore, the appropriate test statistic for this situation is 2.578 .