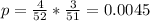Question

Two cards are drawn at random from an ordinary deck of 52 cards. Determine the probability that both cards are jacks if a. the first card is replaced before the second card is drawn.

Answer 1

With replacing

Assuming replacing for the first selection we have a total of 52 cards and 4 possible options and for the second selection since we put again the card again in the deck we have the same probability of selection for a jack. We can assume independence between the events and we got:

`p = (4)/(52) *(4)/(52)= 0.0059`

Without replacing

Assuming replacing for the first selection we have a total of 52 cards and 4 possible options and for the second selection since we don't put again the card again in the deck so we will have 3 possible options and 51 total cards. We can assume independence between the events and we got:

`p = (4)/(52) *(3)/(51)= 0.0045`

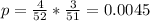
Explanation:

For this case we assume that we have a standard deck of 52 cards

And we have 4 Jacks on the deck

With replacing

Assuming replacing for the first selection we have a total of 52 cards and 4 possible options and for the second selection since we put again the card again in the deck we have the same probability of selection for a jack. We can assume independence between the events and we got:

`p = (4)/(52) *(4)/(52)= 0.0059`

Without replacing

Assuming replacing for the first selection we have a total of 52 cards and 4 possible options and for the second selection since we don't put again the card again in the deck so we will have 3 possible options and 51 total cards. We can assume independence between the events and we got:

`p = (4)/(52) *(3)/(51)= 0.0045`