Question

A train leaves a station and travels north at a speed of 45 ​km/h. Two hours​ later, a second train leaves on a parallel track and travels north at 75 ​km/h. How far from the station will they​ meet?

Answer 1

The trains will meet 225km north from the station.

Step-by-step explanation:

First, we need the equation of position of the two trains. Since they have constant velocities, these equations are:

`x_1=v_1(t+t_0)\\\\x_2=v_2t}`

Where
`t_0` is the time the first train is traveling before the second train levaes the station. When the trains meet,
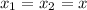`x_1=x_2=x` . If we solve for t in the equations above, we have:

`t=(x)/(v_1)-t_0\\ \\t=(x)/(v_2)`

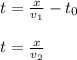
Matching these equations and solving for x, we obtain:

`(x)/(v_1)-t_0=(x)/(v_2)\\\\xv_2-v_1v_2t_0=xv_1\\\\x(v_2-v_1)=v_1v_2t_0\\\\x=(v_1v_2t_0)/(v_2-v_1)\\ \\\implies x=((45km/h)(75km/h)(2h))/(75km/h-45km/h)=225km`

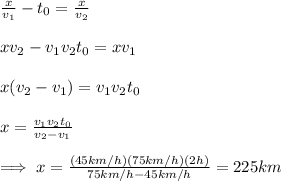
In words, the trains will meet 225km north from the station.