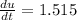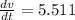Question

A steady, incompressible, two-dimensional velocity field is given by the following components in the x-y plane: u=1.85+2.05x+0.656y v=0.754−2.18x−2.05y . Calculate the acceleration field (find expressions for acceleration components ax and ay), and calculate the acceleration at the point (x,y) = (-1, 4). The acceleration components are ax = + x ay = + y Acceleration components at (-1, 4) are ax = ay =

Answer 1

`(du)/(dt) = 1.515`

`(dv)/(dt) = 5.511`

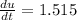
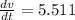
Step-by-step explanation:

The acceleration field is obtained by deriving the components in function of the time. That is to say:

`(du)/(dt)=2.05\cdot (dx)/(dt)+0.656\cdot (dy)/(dt)\\(dv)/(dt) = -2.18\cdot (dx)/(dt) -2.05\cdot (dy)/(dt)`

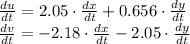
Where
`(dx)/(dt) = u` and
`(dy)/(dt) = v`.

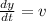The velocity components at given point are, respectively:

`u = 2.424`

`v=-5.266`

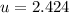
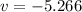
Lastly, the acceleration components are found:

`(du)/(dt) = 1.515`

`(dv)/(dt) = 5.511`