Question

A transformer connected to a 120--V ac line is to supply 12.0V (rms) to a portable electronic device. The load resistance in the secondary is 4.70 ohms

a. What should the ratio of primary to secondary turns of the transformer be?
b. What rms current must the secondary supply?
c. What average power is delivered to the load?
d. What resistance connected directly across the source line (which has a voltage of 120?V ) would draw the same power as the transformer?

Answer 1

Therefore,

a)
`(N_(1))/(N_(2))=(10)/(1)`

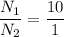
b) I₂ = 2.55 Ampere

c) Power = 30.6 Watts

d) R₁ = 470.58 ohms.

Step-by-step explanation:

Given:

Let the primary voltage be,

`V_(1)=120\ V`

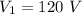
Secondary Voltage,

`V_(2)=12\ V`

Secondary Resistance,

`R_(2)=4.7\ ohms`

To Find:

a)
`(N_(1))/(N_(2))=?`

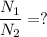
b) I₂ = ?

c) Power = ?

d) R₁ = ?

Solution:

The ratio of primary to secondary turns of the transformer, is the ratio of primary to secondary Voltage and is given by,

`(N_(1))/(N_(2))=(V_(1))/(V_(2))`

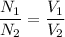
Substituting the values we get

`(N_(1))/(N_(2))=(120)/(12)=(10)/(1)`

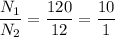
For, rms current for the secondary supply,

`I_(2)=(V_(2))/(R_(2))`

Substituting the values we get

`I_(2)=(12)/(4.7)=2.55\ Ampere`

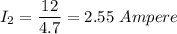
Now for average power at load,

`Power=V_(2)* I_(2)`

Substituting the values we get

`Power=12* 2.55=30.6\ Watts`

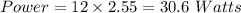
Now for resistance connected directly across the source line Power will remain same,

`Power=((V_(1))^(2))/(R_(1))`

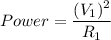
Substituting the values we get

`R_(1)=((V_(1))^(2))/(Power)=(14400)/(30.6)=470.58\ ohms`

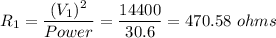
Therefore,

a)
`(N_(1))/(N_(2))=(10)/(1)`

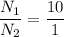
b) I₂ = 2.55 Ampere

c) Power = 30.6 Watts

d) R₁ = 470.58 ohms.