Question

If a publisher of nontechnical books takes great pains to ensure that itsbooks are free of typos, so that the probability of any given page containing at leastone such error is .005 & errors are independent from page to page. What is theprobability that:(a) One of its 400-page novels will contain exactly 1 page with errors? Answer: .271(b) At most three pages are with errors? Answer: .857

Answer 1

(a) The probability of exactly 1 page has error is 0.271.

(b) The probability that there are at most 3 pages has error is 0.857.

Explanation:

Let X = number of typos.

The probability of a typo is, P (X) = p = 0.005.

The number of pages in the novel is, n = 400.

The random variable X follows a Binomial distribution with parameter n and p.

But as the probability is very small and the sample size is too large we can use Poisson distribution to approximate the binomial distribution.

This distribution has parameter,
`\lambda=np=400*0.005=2`.

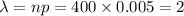The probability mass function of the Poisson distribution is:

`P(X=x)=(e^(-2)2^(x))/(x!) ;\ x=0,1,2,...`

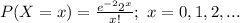
(a)

Compute the probability of exactly 1 page has error as follows:

`P(X=1)=(e^(-2)2^(1))/(1!) =(0.13534*2)/(1) =0.27068\approx0.271`

Thus, the probability of exactly 1 page has error is 0.271.

(b)

Compute the probability that there are at most 3 pages has error as follows:

P (X ≤ 3) = P (X = 0) + P (X = 1) + P (X = 2) + P (X = 3)

`=(e^(-2)2^(0))/(0!)+(e^(-2)2^(1))/(1!)+(e^(-2)2^(2))/(2!)+(e^(-2)2^(3))/(3!)\\=0.13534+0.27067+0.27067+0.18045\\=0.85713\\\approx0.857`

Thus, the probability that there are at most 3 pages has error is 0.857.