Question

Brad is looking out his window daydreaming. The number of people who pass by outside his window per hour is a Poisson random variable (rv) with 0-24. Let Y be the number of people who pass by outside Brad's window during the first hour (a) What is PY-7? (b) Suppose that five people passed by in the first 30 minutes. Given this, what is the probability that Y 17? c) What are E Y and Var(Y)?

Answer 1

(a) The probability of 7 people passing by the window in the first hour is 0.000034.

(b) The probability of Y = 17 is 0.1144.

(c) The value of E (Y) and V (Y) is 24.

Explanation:

Let Y = number of people who passes by Brad's window per hour.

The random variable X follows a Poisson distribution with parameter, λ = 24.

The probability mass function of a Poisson distribution is:

`P(Y=y)=(e^(-24)24^(y))/(y!);\ x=0,1,2,...`

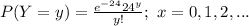
(a)

Compute the value of P (Y = 7) as follows:

`P(Y=7)=(e^(-24)24^(7))/(7!)=(0.17315)/(5040) =0.000034`

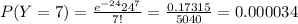
Thus, the probability of 7 people passing by the window in the first hour is 0.000034.

(b)

It is provided that 5 people have already passed by the window in the first 30 minutes.

This implies that in the next 30 minutes 12 people will pass.

The average number of people passing Brad's window in 30 minutes is,
`\lambda=(24)/(2)=12`

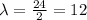
Compute the probability of Y = 17 as follows:

P (Y = 17) = P (12 people passing in the nest 30 minutes)

`=(e^(-12)12^(12))/(12!)=(54782414.52)/(479001600) =0.114368\approx0.1144`

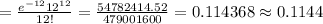
Thus, the probability of Y = 17 is 0.1144.

(c)

The expected value and variance of a Poisson distribution are same as λ.

So,

E (Y) = 24

V (Y) = 24

Thus, the value of E (Y) and V (Y) is 24.