Question

A lamina occupies the part of the disk x2+y2≤4 in the top half. Find its mass if the density at any point is 2.3 times the point's distance from the origin.

Answer 1

Answer: Its mass is 9.2 if the density at any point is 2.3 times the point's distance from the origin.

Explanation:

Since we have given that

`x2+y2\leq 4`

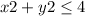
Take polar coordinate:

`x=r\cos \theta\\\\y=r\sin \theta`

And we know that

`x^2+y^2=r^2\\\\dA=rdrd\theta`

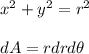
So, it becomes,

`0\leq r^2\leq 4\\\\0\leq r\leq 2`

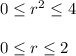
Since density at any points is 2.3 times the point's distance from the origin.

`\rho=2.3(√(x^2+y^2))^2\\\\\rho=2.3(x^2+y^2)\\\\\rho=2.3r^2`

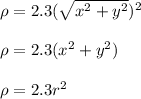
So, the mass of the lamina is given by

`m=\int\limits^a_b \int\limits^a_b {\rho} dA\\\\m=\int\limits^(2\pi )_(\pi)\int\limits^2_0 {2.3r^2.r} \, drd\theta\\\\m=2.3\int\limits^(2\pi )_(\pi) \, d\theta\int\limits^2_0 {r^3} \, dr\\\\m=2.3[\theta]_(\pi)^(2\pi)* [(r^4)/(4)]_2^0\\\\m=(2.3)/(4)(2\pi-\pi)(16-0)\\\\m=(2.3\pi)/(4)* 16\\\\m=2.3* 4=9.2`

Hence, its mass is 9.2 if the density at any point is 2.3 times the point's distance from the origin.