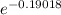Answer:
The time for the cake to cool off to room temperature is
approximately 30 minutes.
Let
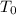 =
=
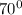 F be the temperature and T that of the body
F be the temperature and T that of the body
Step-by-step explanation:
Our Tm = 70, the initial-value problem is
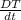 = k(T − 70), T(0) = 300
= k(T − 70), T(0) = 300
Solving the equation, we get
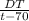 = kdt
= kdt
In [T-70]= kt +
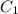
T = 70 +
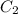
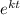
Finding he value for
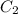 using the initial value of T (0)= 300, therefore we get:
using the initial value of T (0)= 300, therefore we get:
300=70+
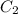
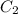 = 230 therefore
= 230 therefore
T= 70+ 230
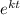
Finding the value for k using T (3) = 200, therefore we get
T (3) = 200
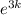 =
=
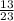
K =
 in
in
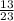
= -0.19018
Therefore
T(t) = 70+230