Question

Newsweek in 1989 reported that 60% of young children have blood lead levels that could impair their neurological development. Assuming a random sample from the population of all school children at risk, find the probability that at least 5 children out of 10 in a sample taken from a school may have a blood level that may impair development.

Answer 1

To find the probability that at least 5 children out of 10 in a sample may have a blood level that may impair development, we can use the binomial probability formula. The probability of at least 5 children having blood lead levels that may impair development is approximately 0.5616.

Step-by-step explanation:

To find the probability that at least 5 children out of 10 in a sample may have a blood level that may impair development, we can use the binomial probability formula. Considering that the probability of a child having a blood lead level that may impair development is 60%, we need to calculate the probability of having 5 or more successes in a sample of 10.

Using a binomial probability calculator, we can find that the probability of having exactly 5, 6, 7, 8, 9, or 10 successes is approximately 0.5616. This means that the probability of at least 5 children having blood lead levels that may impair development is approximately 0.5616.

Answer 2

The answer is 83.38%.

Step-by-step explanation:

The probability of young children having blood levels that impair their neurological development is given as 60% in the question. To find the probability of at least 5 children out of 10 in a sample having said blood levels, we need to use the binomial probability.

n represents the total number of children in the sample so n = 10 and p is the probability of the children having blood levels causing the problem which is 60% so p = 0.6.

We want the probability of it being observed for 5 or more children and that is
`P(x\geq 5)`. If we subtract the
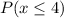`P( x\leq 4)` from 1, which is the probability of not observing the condition in 5 or more children, we will have the
`P(x\geq 5)`.

`1 - P(x\leq 4) = 1 - pbinom(4, 10, 0.6)` which are the probability range in the function, the sample size and the probability of observing the condition respectively.

The result is 1 - 0.1662 = 0.8338 which means that the probability that is asked is 83.38%.

I hope this answer helps.