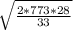Question

A produce distributor uses 773 packing crates a month, which it purchases at a cost of $11 each. The manager has assigned an annual carrying cost of 33 percent of the purchase price per crate. Ordering costs are $28. Currently the manager orders once a month. How much could the firm save annually in ordering and carrying costs by using the EOQ?

Answer 1

`\sqrt(2*773*28)/(33)`Answer:

Step-by-step explanation:

Using the EOQ Formula = EOQ
`\sqrt(2*D*O)/(H)`

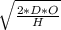
D = Demand = 773

O = Ordering Cost =28

H = holding Cost = 11*33% =3.63

So we have :

EOQ=
`\sqrt(2*D*O)/(H)`

EOQ=
`\sqrt(2*773*28)/(3.63)`

EOQ=
`\sqrt(43288\\)/(3.63)`

EOQ=
`√(11925.06887)`

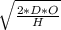
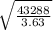
EOQ= 109.20196

Previous per unit order cost = 28/773 =0.03622

No of Orders = D/o

No of Orders = 773/109.20196 =7.0786

Cost per order =109.20196*0.03622 =3.9555

Total order cost= 7.0786*3.9555=27.9998

At EOQ holding Cost is equal to Order Cost

New Order cost =27.9998

Holding Cost = 27.9998

New cost As per EOQ = 56

Previous (33+28) = 61

Net Saving = 5