Answer:
Force is 161.27 N and frequency of vibration when the string vibrates in three segments is 660 Hz .
Step-by-step explanation:
Given :
Frequency , f = 220 Hz .
Length of wire , L = 70 cm = 0.7 m .
Mass of wire ,
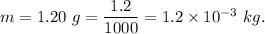
a ) We know, frequency in string is :
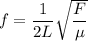
Therefore ,
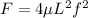 .... equation 1.
.... equation 1.
Here ,
 is mass per unit length .
is mass per unit length .
So,
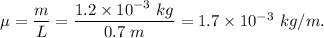
Putting value of
 in equation 1.
in equation 1.
We get ,
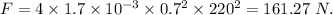
b) We know , frequency of when n segment are in string :
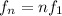
For , n = 3

Hence , this is the required solution.