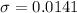Answer:

We can calculate the sample variance with the following formula:
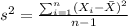
And replacing we got:
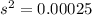
And the deviation is given by this:
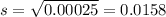
If we want to find the population deviation we just need to use this formula:
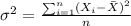
And replacing we got:
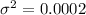
And the population deviation would be:
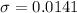
Explanation:
For this case we have the following values:
0.14, 0.15, 0.16, 0.17, 0.18.
We can calculate the mean with the following formula:

And replacing we got:

We can calculate the sample variance with the following formula:
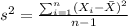
And replacing we got:
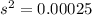
And the deviation is given by this:
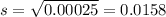
If we want to find the population deviation we just need to use this formula:
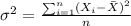
And replacing we got:
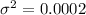
And the population deviation would be: