Question

Deer ticks can carry both Lyme disease and human granulocytic ehrlichiosis (HGE). In a study of ticks in the Midwest, it was found that 16% carried Lyme disease, 10% had HE, and that 10% of the ticks that had either Lyme disease or HGE carried both diseases.

(a) What is the probability that a tick carries both Lyme disease (L) and HE (H)?

(b) What is the conditional probability that a tick has HE given that it has Lyme disease?

Answer 1

(a) 0.16

(b) 1

Step-by-step explanation:

Let Probability that ticks in the Midwest carried Lyme disease, P(L) = 0.16

Probability that ticks in the Midwest carried HGE disease, P(H) = 0.10

Probability that ticks in the Midwest carried either Lyme disease or HGE disease, P(
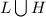`L \bigcup H`) = 0.10

(a) Probability that a tick carries both Lyme disease (L) and HE (H) is given by

P(L
`\bigcap` H);

As we know that P(A
`\bigcup` B) = P(A) + P(B) - P(A
`\bigcap` B)

So, in our question;

P(L
`\bigcup` H) = P(L) + P(H) - P(L
`\bigcap` H)

0.10 = 0.16 + 0.10 - P(L
`\bigcap` H)

P(L
`\bigcap` H) = 0.16 + 0.10 - 0.10 = 0.16

Therefore, the probability that a tick carries both Lyme disease (L) and HE (H) is 0.16 or 16% .

(b) Conditional Probability P(A/B) is given by =
`(P(A\bigcap B))/(P(B))`

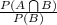
So, the conditional probability that a tick has HE given that it has Lyme disease is given by = P(H/L)

P(H/L) =
`(P(H\bigcap L))/(P(L))` =
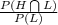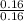`(0.16)/(0.16)` = 1 .