Question

A new DVD is available for sale in a store one week after its release. The cumulative revenue,

$R, from sales of the DVD in this store in week t after its release is


R=f(t)=260 ln t with t>1.Find f(2), f
​′
​​
(2), and the relative rate of change
​f
​
​f
​′
​​
​​
at t=2.

f(2)=?

f
​′
​​
(2)=?

​f
​
​f
​′
​​
​​
= ?



Interpret your answers in terms of revenue. Round the last answer to one decimal place. (Choose from available answers in parentheses.)



Two weeks after the DVD was released,

the revenue from sales is $____?_____.

and is (increasing/decreasing)

at a rate of $___?____ per week,

or ___?____% per week.

Answer 1

f(2) = $180.22

f'(2) = $130.00/week

f'(2)/f(2) = 72.13%

Two weeks after the DVD was released, the revenue from sales is $180.22 and is increasing at a rate of $130 per week, or 72.13% per week.

Explanation:

The revenue from sales, in dollars, as a function of time, in weeks, is given by:

`f(t)=260ln(t)`

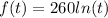
After two weeks (t=2), the revenue from sales is:

`f(2)=260ln(2)\\f(2) = \$180.22`

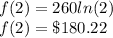
The rate of change, which is given by the derivate of the revenue function, at t = 2 weeks is:

`f'(t)=(d)/(dt) 260ln(t)\\f'(t) = (260)/(t)\\f'(2) = (260)/(2)=\$130.00/week`

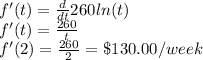
The relative rate of change is:

`(f'(2))/(f(2))=(130)/(180.22)=0.7213=72.13\%`

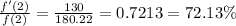
Therefore, Two weeks after the DVD was released, the revenue from sales is $180.22 and is increasing at a rate of $130 per week, or 72.13% per week.