Question

How many times must we toss a coin to ensure that a 0.95-confidence interval for the probability of heads on a single toss has length less than 0.1, 0.05, and 0 .01, respectively

Answer 1

(1) 97

(2) 385

(3) 9604

Explanation:

The (1 - α) % confidence interval for population proportion is:

`CI=\hat p\pm z_(\alpha/2)\sqrt{(\hat p(1-\hat p))/(n)}`

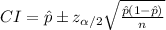
The margin of error in this interval is:

`MOE= z_(\alpha/2)\sqrt{(\hat p(1-\hat p))/(n)}`

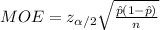
The formula to compute the sample size is:

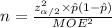
`\\n=(z_(\alpha/2)^(2)* \hat p(1-\hat p))/(MOE^(2))`

(1)

Given:

`\hat p = 0.50\\MOE=0.1\\z_(\alpha/2)=z_(0.05/2)=z_(0.025)=1.96`

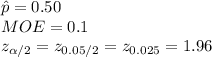
*Use the z-table for the critical value.

Compute the value of n as follows:

`\\n=(z_(\alpha/2)^(2)* \hat p(1-\hat p))/(MOE^(2))\\=(1.96^(2)*0.50*(1-0.50))/(0.1^(2))\\=96.04\\\approx97`

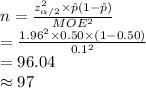
Thus, the minimum sample size required is 97.

(2)

Given:

`\hat p = 0.50\\MOE=0.05\\z_(\alpha/2)=z_(0.05/2)=z_(0.025)=1.96`

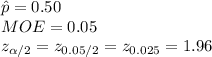
*Use the z-table for the critical value.

Compute the value of n as follows:

`\\n=(z_(\alpha/2)^(2)* \hat p(1-\hat p))/(MOE^(2))\\=(1.96^(2)*0.50*(1-0.50))/(0.05^(2))\\=384.16\\\approx385`

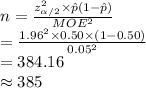
Thus, the minimum sample size required is 385.

(3)

Given:

`\hat p = 0.50\\MOE=0.01\\z_(\alpha/2)=z_(0.05/2)=z_(0.025)=1.96`

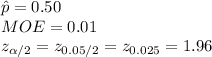
*Use the z-table for the critical value.

Compute the value of n as follows:

`\\n=(z_(\alpha/2)^(2)* \hat p(1-\hat p))/(MOE^(2))\\=(1.96^(2)*0.50*(1-0.50))/(0.01^(2))\\=9604`

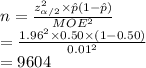
Thus, the minimum sample size required is 9604.