Question

To save money, a local charity organization wants to target its mailing requests for donations to individuals who are most supportive of its cause. They ask a sample of 5 men and 5 women to rate the importance of their cause on a scale from 1 (not important at all) to 7 (very important). The ratings for men wereM1 = 6.1.The ratings for women were M2 = 4.9. If the estimated standard error for the difference (sM1 − M2) is equal to 0.25, then consider the following.Find the confidence limits at an 80% CI for these two-independent samples. (Round your answers to two decimal places

Answer 1

The 80% confidence interval for difference between two means is (0.85, 1.55).

Explanation:

The (1 - α) % confidence interval for difference between two means is:

`CI=(\bar x_(1)-\bar x_(2))\pm t_{\alpha/2,(n_(1)+n_(2)-2)}* SE_{\bar x_(1)-\bar x_(2)}`

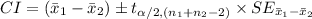
Given:

`\bar x_(1)=M_(1)=6.1\\\bar x_(2)=M_(2)=4.9\\SE_{\bar x_(1)-\bar x_(2)}=0.25`

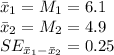
Confidence level = 80%

`t_{\alpha/2, (n_(1)+n_(2)-2)}=t_(0.20/2, (5+5-2))=t_(0.10,8)=1.397`

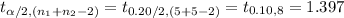
*Use a t-table for the critical value.

Compute the 80% confidence interval for difference between two means as follows:

`CI=(6.1-4.9)\pm 1.397* 0.25\\=1.2\pm 0.34925\\=(0.85075, 1.54925)\\\approx(0.85, 1.55)`

Thus, the 80% confidence interval for difference between two means is (0.85, 1.55).