Question

Total profit from marginal profit. Stevens Bakery has found that its marginal profit, in dollars per wedding cake, is

C'(x) - 0.12x + 40,

where x is the number of wedding cakes produced. Find the total profit from producing 50 wedding cakes.

Answer 1

2150 Profit at 50 cakes quantity

Explanation:

Marginal Profit [C'(x)] is Addition to total profit due to increase in quantity 'x'. So it is derivation of 'total profit function' with respect to 'quantity x'= ∂TP/∂x. Hence, Total Profit is integration of Marginal Profit with respect to x.

Marginal Profit : C'(x) = -0.12x + 40

Total Profit : C (x) = ∫-0.12x + 40

= -0.12x^2 / 2 + 40x

Total Profit Function = 0.06x^2 + 40x

Total Profit at given quantity = 50 cakes :

0.06 (50)^2 + 40 (50)

0.06 (2500) + 2000

150 + 2000

= 2150 [ Profit at 50 cakes quantity ]

Answer 2

The total profit from producing 50 wedding cakes is 2,150 dollars

Explanation:

Stevens Bakery has found that its marginal profit, in dollars per wedding cake, is
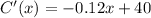`C'(x) = - 0.12 x + 40` , where x is the number of wedding cakes produced

From the given information:

C'(x) = - 0.12 x + 40

Integrate both sides we get,

`\int C'(x) dx = \int (-0.12x+40)dx`
`\int x^n dx = (x^(n+1))/(n+1)+C`

`C(x) = -0.12 * (x^(2))/(2)+40x`

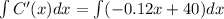
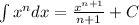
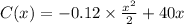
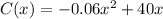`C(x) = -0.06x^2+40x` ...... (1)

Substitute the value of x=50 wedding cakes in equation (1) as shown below:

`C(50) = -0.06 (50)^2 +40(50) = 150+2000`

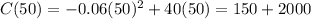
=2,150 dollars

Hence, the total profit from producing 50 wedding cakes is 2,150 dollars.