We are given the following equation and want to solve for x:
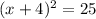
We could expand the (x+4)², but we're going to take the square root of both sides since that would be much more simpler.
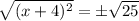
Remember to add the plus/minus symbol when taking the square root of both sides when solving for such equations.
After taking the square root of both sides, we have two equations, one with the positive instance and one with the negative instance.
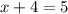 AND
AND
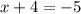
Subtract both sides of both equations by 4
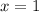 AND
AND

These are both solutions to the equation. Let me know if you need any clarifications, thanks!
~ Padoru