Question

Find the volume of the solid generated by revolving the region bounded above by yequals12 cosine x and below by yequals3 secant x​, negative StartFraction pi Over 3 EndFraction less than or equals x less than or equals StartFraction pi Over 3 EndFraction about the​ x-axis.

Answer 1

Explanation:

The curves and the region bounded are shown in the attachment.

The region is revolved around x axis.

We have to find the volume of the resulting solid

Limits for x are
`(-\pi)/(3) ,(\pi)/(3)`

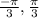
The region lies above 3 secx =y and below y= 12 cos x

So volume=
`\pi\int\limits_ {(-\pi)/(3)} ^ {(\pi)/(3)} \, (12cosx)^2 - (3 secx)^2 dxdx \\= \pi \int\limits_ {(-\pi)/(3)} ^ {(\pi)/(3)} (144 cos^2 x dx -9 sec^2 x dx)\\= \pi \int\limits_ {(-\pi)/(3)} ^ {(\pi)/(3)}(72 +72 cos2x -9sec^2 x )dx\\= 72 +36 sin 2x -9 tanx`

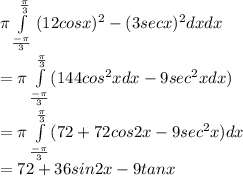
substitute limits

=
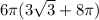`6\pi (3√(3) +8\pi)` cubic units