Question

A sky diver of mass 53 kg can slow herself to a constant speed of 95 km/h by orienting her body horizontally, looking straight down with arms and legs extended. In this position, she presents the maximum cross-sectional area and thus maximizes the air-drag force on her.

(a) What is the magnitude of the drag force on the sky diver?
N
(b) If the drag force is equal to bv2, what is the value of b?
kg/m
(c) At some instant she quickly flips into a "knife" position, orienting her body vertically with her arms straight down. Suppose this reduces the value of b to 55 percent of the value in Parts (a) and (b). What is her acceleration at the instant she achieves the "knife" position?
m/s2

Answer 1

force = 520 N

b = 0.747 kg/m

acceleration = 4.41 m/s²

Step-by-step explanation:

given data

mass = 53 kg

speed = 95 km/h

solution

as here driver is at constant speed so here drag force is

drag force = mg

force = 53 × 9.81

force = 520 N

and when drag force is equal to bv²

b =
`(mg)/(v^2)`

b =
`(520)/(26.38)`

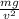
b = 0.747 kg/m

and

here x = 520 × 0.55 = 286 N

so here

F net = 520 - 286

F net = 234 N

so here

acceleration =
`(F \ net)/(m)`

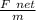
acceleration =
`(234)/(53)`

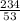
acceleration = 4.41 m/s²