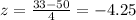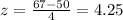Answer:
a)
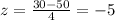
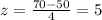
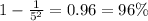
b)
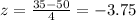
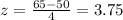
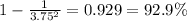
c)

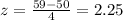
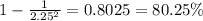
d)
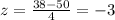

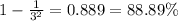
e)
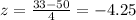
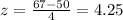

Explanation:
Data given
 reprsent the population mean
reprsent the population mean
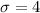 represent the population standard deviation
represent the population standard deviation
The Chebyshev's Theorem states that for any dataset
• We have at least 75% of all the data within two deviations from the mean.
• We have at least 88.9% of all the data within three deviations from the mean.
• We have at least 93.8% of all the data within four deviations from the mean.
Or in general words "For any set of data (either population or sample) and for any constant k greater than 1, the proportion of the data that must lie within k standard deviations on either side of the mean is at least:
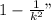
Part a
For this case we can find the deviations from the mean like this:
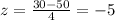
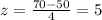
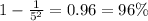
Part b
For this case we can find the deviations from the mean like this:
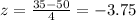
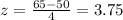
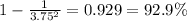
Part c
For this case we can find the deviations from the mean like this:

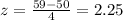
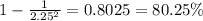
Part d
For this case we can find the deviations from the mean like this:
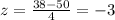

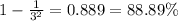
Part e
For this case we can find the deviations from the mean like this: