Question

Person exerts a 11-N force on a cart attached to a spring and holds the cart steady. The cart is displaced 0.060 m from its equilibrium position. When the person stops holding the cart, the system+spring undergoes simple harmonic motion.

1. Determine the spring constant of the spring.
2. Determine the total energy of the system.
3. Write an expression x(t) for the motion of the cart. Assume the frequency f=1Hz. Express your answer in terms of the variable t and constant pi.

Answer 1

1. k = 183.33 N/m

2. E = 0.33 J

3. x(t) = 0.06cos(2πt)

Step-by-step explanation:

1. Determine the spring constant of the spring.

To determine the spring constant, we use hooke's law:

F = kΔx

where

F is the force = 11 N

Δx is the displacement = 0.06 m

k is the spring constant

k = F/Δx

k = 11/0.06 = 183.33 N/m

2. Determine the total energy of the system

the total energy(E) =
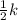`(1)/(2)k`Δ
`x^(2)` = 0.5 × 183.33 × 0.06² = 0.33 J.

Therefore the total energy of the system is 0.33 J

3. Write an expression x(t) for the motion of the cart. Assume the frequency f=1Hz. Express your answer in terms of the variable t and constant pi.

The expression for the motion of the cart x(t) is given by:

x(t) = Δxcos(2πft)

where the frequency f = 1 Hz

x(t) = 0.06cos(2π ×1 × t)

x(t) = 0.06cos(2πt)