Question

A box of mass 3.1kg slides down a rough vertical wall. The gravitational force on the box is 30N . When the box reaches a speed of 2.5m/s , you start pushing on one edge of the box at a 45? angle (use degrees in your calculations throughout this problem) with a constant force of magnitude Fp = 23N , as shown in figure. (Figure 1) There is now a frictional force between the box and the wall of magnitude 13N . How fast is the box sliding 2.0s after you started pushing on it?

Using our simplified model, in which we know that the forces are constant (but we don't know what their magnitudes are), which of the following motion diagrams would be a reasonable representation of the motion of the box?

Answer 1

The speed of the box after 2 s is 3 m/s.

Step-by-step explanation:

The net force on the box in vertical direction:

`{F_(net)} = {F_g} - f - {F_p}\sin {45^{\rm{o}}}F`

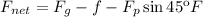
Here,
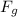`{F_g}` is the gravitational force, f is the force of friction and
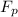`{F_p}` is the pushing force.

According to Newton’s second law, the net force is:

`{F_(net)} = ma`

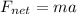
Here, a is the acceleration in vertical direction

`\begin{array}{c}\\ \Rightarrow ma = {F_g} - f - {F_p}\sin {45^{\rm{o}}}\\\\a = \frac{{{F_g} - f - {F_p}\sin {{45}^{\rm{o}}}}}{m}\\\end{array}`

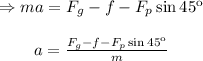
Substitute 30N for Fg, 13N for f and 23N for Fp

`\begin{array}{c}\\a = \frac{{\left( {30{\rm{ N}}} \right) - \left( {13{\rm{ N}}} \right) - \left( {23{\rm{ N}}} \right)\sin {{45}^{\rm{o}}}}}{{3.1{\rm{ kg}}}}\\\\ = \frac{{0.7365{\rm{ N}}}}{{3.1{\rm{ kg}}}}\\\\ = 0.24\;{\rm{m/}}{{\rm{s}}^{\rm{2}}}\\\end{array}`

Newton’s equation of motion:

`v - u = at`

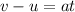
Substitute 2.5m/s for u , 0.24m/s2 for a and 2s for t .

`\begin{array}{c}\\v - 2.5{\rm{ m/s}} = \left( {0.24{\rm{ m/}}{{\rm{s}}^2}} \right)\left( {2{\rm{ s}}} \right)\\\\v = 0.48{\rm{ m/s}} + 2.5{\rm{ m/s}}\\\\ = 2.98{\rm{ m/s}}\\\\ \approx {\bf{3 m}}{\rm{/}}{\bf{s}}\\\end{array}`

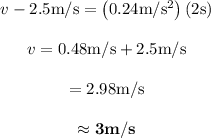
The speed of the box after 2 s is 3 m/s.

Answer 2

The box will be moving at 0.45m/s. The solution to this problem requires the knowledge and application of newtons second law of motion and the knowledge of linear motion. The vertical component of the force Fp acts vertically upwards against the directio of motion. This causes a constant upward force of 23sin45° to act on the box. Fhe frictional force of 13N also acts vertically upwards and so two forces act upwards against rhe force of gravity resulting un a net force of 0.7N acting kn the box. This corresponds to an acceleration of 0.225m/s². So in w.0s after i start to push v = 0.45m/s.

Step-by-step explanation: