Question

Let the weak signal X be a random variable with mean and variance P, and the observations be Y1 = X + Z1 (Z1 being the strong interference), and Y2 = Z1 + Z2 (Z2 is a measurement noise), where Z1 and Z2 are zero mean with variances N1 and N2, respectively. Assume that X, Z1 and Z2 are uncorrelated. Find the MMSE linear estimate of X given Y1 and Y2 and its MSE. Interpret the results.

Answer 1

The linear estimate of MMSE and MSE are given as

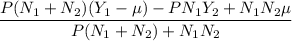`(P(N_1+N_2)(Y_1-\mu)-PN_1Y_2+N_1N_2\mu)/(P(N_1+N_2)+N_1N_2)` and
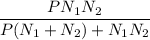`(PN_1N_2)/(P(N_1+N_2)+N_1N_2)` respectively.

Step-by-step explanation:

This is a vector MSE linear estimation problem. Since Z1 and Z2 are zero mean, µY1 = µX +µZ1 =µ and µY2 = µZ1 + µZ2 = 0 . We first normalize the random variables by subtracting their means to get

X' = X − µ and
`Y' =\left[\begin{array}{c}Y_1-\mu\\Y_2\end{array}\right]`

To find the best linear MSE estimate X of X', we first find

`\sum_Y =\left[\begin{array}{cc}P+N1 &N1\\N1 & N1+N2\end{array}\right]`

and

`\sum_( YX)=\left[\begin{array}{c}P\\0\end{array}\right]`

Therefore

`\hat{X}'=\sum_(YX)^T\sum_(Y)^(-1)Y'\\\hat{X}'=\left[\begin{array}{cc}P&0\end{array}\right](1)/(P(N_1+N_2)+N_1N_2)\left[\begin{array}{cc} N_1+N_2 &-N_1\\-N_1 &P+N_1\end{array}\right] Y'\\\hat{X}'=(P)/(P(N_1+N_2)+N_1N_2)\left[\begin{array}{cc} N_1+N_2 &-N_1\end{array}\right]\left[\begin{array}{c}Y_1-\mu\\Y_2\end{array}\right]`

`\hat{X}'=(P(N_1+N_2)(Y_1-\mu)-PN_1Y_2)/(P(N_1+N_2)+N_1N_2)`

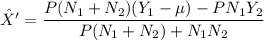
The best linear MSE estimate is Xˆ = Xˆ' + µ. Thus

`\hat{X}=\hat{X}'+\mu\\\hat{X}=(P(N_1+N_2)(Y_1-\mu)-PN_1Y_2)/(P(N_1+N_2)+N_1N_2)+\mu\\\hat{X}=(P(N_1+N_2)(Y_1-\mu)-PN_1Y_2+N_1N_2\mu)/(P(N_1+N_2)+N_1N_2)`

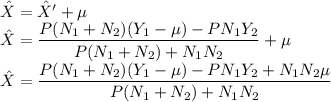
The MSE can be calculated by

`MSE=\sigma_X^2-\sum_(YX)^T\sum_(Y)^(-1)\sum_(YX)`

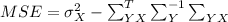
By substituting the values in the above equation as

`MSE=\sigma_X^2-\sum_(YX)^T\sum_(Y)^(-1)\sum_(YX)\\MSE=P-(P)/(P(N_1+N_2)+N_1N_2)\left[\begin{array}{cc} N_1+N_2 &-N_1\end{array}\right]\left[\begin{array}{c}P\\0\end{array}\right]\\MSE=P-(P^2(N_1+N_2))/(P(N_1+N_2)+N_1N_2)\\MSE=(PN_1N_2)/(P(N_1+N_2)+N_1N_2)`

Note that if either N1 or N2 go to 0, the MSE also goes to 0. This is because the estimator will then use the measurement with zero noise variance (that is, the one with no noise) to perfectly reconstruct X.