Question

More people are using social media to network, rather than phone calls or e-mails (US News & World Report, October 20, 2010). From an employment perspective, jobseekers are no longer calling up friends for help with job placement, as they can now get help online. In a recent survey of 150 jobseekers, 67 said they used LinkedIn to search for jobs. A similar survey of 140 jobseekers, conducted three years ago, had found that 58 jobseekers had used LinkedIn for their job search. Use Table 1.

Let p1 represent the population proportion of recent jobseekers and p2 the population proportion of job seekers three years ago. Let recent survey and earlier survey represent population 1 and population 2, respectively.



a. Set up the hypotheses to test whether there is sufficient evidence to suggest that more people are now using LinkedIn to search for jobs as compared to three years ago.
H0: p1 − p2 ≥ 0; HA: p1 − p2 < 0
H0: p1 − p2 ≤ 0; HA: p1 − p2 > 0
H0: p1 − p2 = 0; HA: p1 − p2 ≠ 0


b.
Calculate the value of the test statistic. (Round intermediate calculations to 4 decimal places and final answer to 2 decimal places.)



Test statistic


c. Calculate the critical value at the 5% level of significance. (Round your answer to 3 decimal places.)


Critical value


d. Interpret the results.
Do not reject H0; there is no increase in the proportion of people using LinkedIn
Do not reject H0; there is an increase in the proportion of people using LinkedIn
Reject H0; there is no increase in the proportion of people using LinkedIn
Reject H0; there is an increase in the proportion of people using LinkedIn

Answer 1

Explanation:

Hello!

The objective is to test if the proportion of people that use social media to seek a job has increased in the last three years.

X₁: Number of job seekers that use social media to look form employment presently out of 150.

X₂: Number of job seekers that use social media to look form employment three years ago out of 140.

a.

The claim is that the proportion of job seekers that use social media has increased, then the hypotheses are:

H₀: p₁ - p₂ ≤ 0

H₁: p₁ - p₂ > 0

α: 0.05

b.

`Z_(H_0)= \frac{(p'_1-p'_2)-(p_1-p_2)}{\sqrt{p'(1-p')[(1)/(n_1) +(1)/(n_2)] } }`

Sample population to X₁: p'₁= 67/150= 0.45

Sample population to X₂: p'₂= 58//140= 0.41

Pooled sample proportion p'= (67+58)/(150+140)= 0.43

`Z_(H_0)= \frac{(0.45-0.41)-0}{\sqrt{0.43*0.57*[(1)/(150) +(1)/(140) ]} } = 0.6875= 0.69`

c.

This test is one-tailed to the right, wich means you will reject the null hypothesis at big values of Z:

`Z_(1-\alpha )= Z_(0.95)= 1.648`

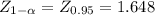
The decision rule using the critical value approach is:

If
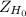`Z_(H_0)` < 1.648, then you don't reject the null hypothesis.

If
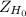`Z_(H_0)` ≥ 1.648, then you reject the null hypothesis.

d.

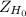`Z_(H_0)` < 1.648, the decision is to reject the null hypothesis.

Then with a level of 5%, there is not enough evidence to reject the null hypothesis. The conclusion is that the proportion of people that seek jobs using social media either hasn't changed or is less than three years ago.

I hope it helps!