Question

Consider a simple poll that is measuring the proportion of citizens that hold a particular political belief. What is a conservative, "worst case scenario" sample size if you want the margin of error to be 3.4%?

Answer 1

Explanation:

Hello!

The proportion is a parameter of a binomial distribution. When studying it, when there is no prior information to base your assumptions or pilot test that will give you an idea of the value the proportion might take, you have to assume the "worst-case scenario". This means, that the probabilities of "failure" and "success" of the experiment are equal, meaning, both have a 50% chance fo occurring.

So with this in mind, you have to calculate the sample size using a hypothetical sample proportion of p'=0.5

To estimate the population proportion using a confidence interval you have to use an approximation to the standard normal distribution, the general structure of the formula is "point estimator" ± "margin of error", in this example:

p' ±
`Z_(1-\alpha /2) * \sqrt{(p'(1-p'))/(n) }`

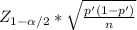
I'll set a Confidence Level fo 95% so
`Z_(1-\alpha /2)= Z_(0.975)= 1.965`

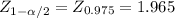
The sample size must be for a margin of error of d= 0.034

d=
`Z_(1-\alpha /2) * \sqrt{(p'(1-p'))/(n) }`

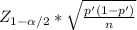
d *
`Z_(1-\alpha /2)` =
`\sqrt{(p'(1-p'))/(n) }`

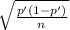
(d *
`Z_(1-\alpha /2)`)²=
`(p'(1-p''))/(n)`

n*(d *
`Z_(1-\alpha /2)`)²= p'(1-p')

n=
`(p'(1-p'))/((d*Z_(1-\alpha /2))^2)`

`n= (0.5*0.5)/((0.034*1.965)^2)`

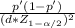
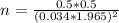
n= 56

Using a confidence level of 95% you have to take a sample size of n= 56

I hope it helps!