Question

At a certain airport, 65% of the flights arrive on time. A sample of 10 flights is studied. Find the probability that all 10 of the flights were on time.

Answer 1

So, the probability is P=0.0135.

Explanation:

We know that at a certain airport, 65% of the flights arrive on time.

We get that p=0.65 and q=1-0.65=0.35.

We have 10 flights, so n=10.

We calculate the probability that all 10 of the flights were on time, so k=10.

We use the formulu:

`\boxed{P(X=k)=C^n_k \cdot p^k\cdot q^(n-k)}`

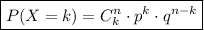
we get:

`P(X=10)=C^(10)_(10)\cdot 0.65^(10)\cdot 0.35^0\\\\P(X=10)=1\cdot 0.0135\cdot 1\\\\P(X=10)=0.0135\\`

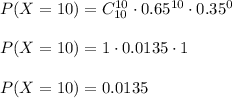
So, the probability is P=0.0135.