Question

Binomial probability distributions depend on the number of trials n of a binomial experiment and the probability of success p on each trial. Under what conditions is it appropriate to use a normal approximation to the binomial? (Select all that apply.)

np > 5
p < 0.5
p > 0.5
nq > 5
np > 10
nq > 10

Answer 1

Correct options: np > 10, nq > 10 and p < 0.50.

Explanation:

Let X be discrete binomial random variable.

The probability of success is p and the number of independent trials is n.

The probability mass function of a Binomial distribution is:

`P(X=x)={n\choose x}p^(x)(1-p)^(n-x);\ x=0,1,2,3...`

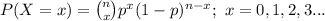
In case, the sample size is too large, i.e. n > 30 and the probability of success is too small, i.e. p < 0.50, then the Normal distribution can be used to approximate the Binomial distribution.

The conditions to be satisfied for Normal approximation are:

• 
  `np>10\\`
• 
  `n(1-p)>10`

Thus, the correct options are np > 10, nq > 10 and p < 0.50.