Question

Choose the equivalent system of linear equations that will produce the same solution as the one given below. (1 point) 4x − 2y = 6 2x + y = 5 Select one: a. −4x − 2y = 10 −4y = 4 b. −4x − 5y = −1 −7y = 5 c. 3x + 2y = 6 7x = 12 d. 4x + 2y = 10 8x = 16

Answer 1

Option d) 4x + 2y = 10 and 8x = 16 is correct

Therefore 4x + 2y = 10 and 8x = 16 equations have equivalent solution (2,1) is same as the solution of given linear system of equations

Explanation:

Given equations are

`4x-2y=6\hfill (1)`

`2x+y=5\hfill (2)`

To find the the equivalent system of linear equations that will produce the same solution as for the given equation :

First find the solution to the given system of equations by elimination method

Multiply the equation (2) into 2 we get

`4x+2y=10\hfill (3)`

Now adding the equations (1) and ( 3) we get

`4x-2y=6`

`4x+2y=10`

_______________

`8x=16`

`x=(16)/(8)`

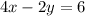
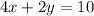
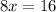
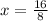
x=2

Therefore the value of x is 2

Substitute the value of x in equation (1) we get

`4(2)-2y=6`

`8-2y=6`

`-2y=6-8`

`-2y=-2`

`y=(-2)/(-2)`

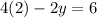
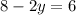
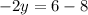
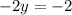
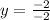
y=1

Therefore the value of y is 1

Therefore the solution to the given system of equations is (2,1)

Now to find the equivalent system of equations have same solution (2,1)

Verify the equations
`4x+2y=10\hfill (4)` and 8x = 16

From 8x=16

`x=(16)/(8)`

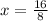
x=2

Therefore the value of x is 2

Substitute x=2 in equation (4) we get

4(2)+2y=10

8+2y=10

2y=10-8

2y=2

`y=(2)/(2)`

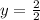
y=1

Therefore the value of y is 1

Therefore the solution is (2,1)

Therefore option d) 4x + 2y = 10 and 8x = 16 equations have equivalent solution (2,1) is same as the solution of given linear system of equations